
|
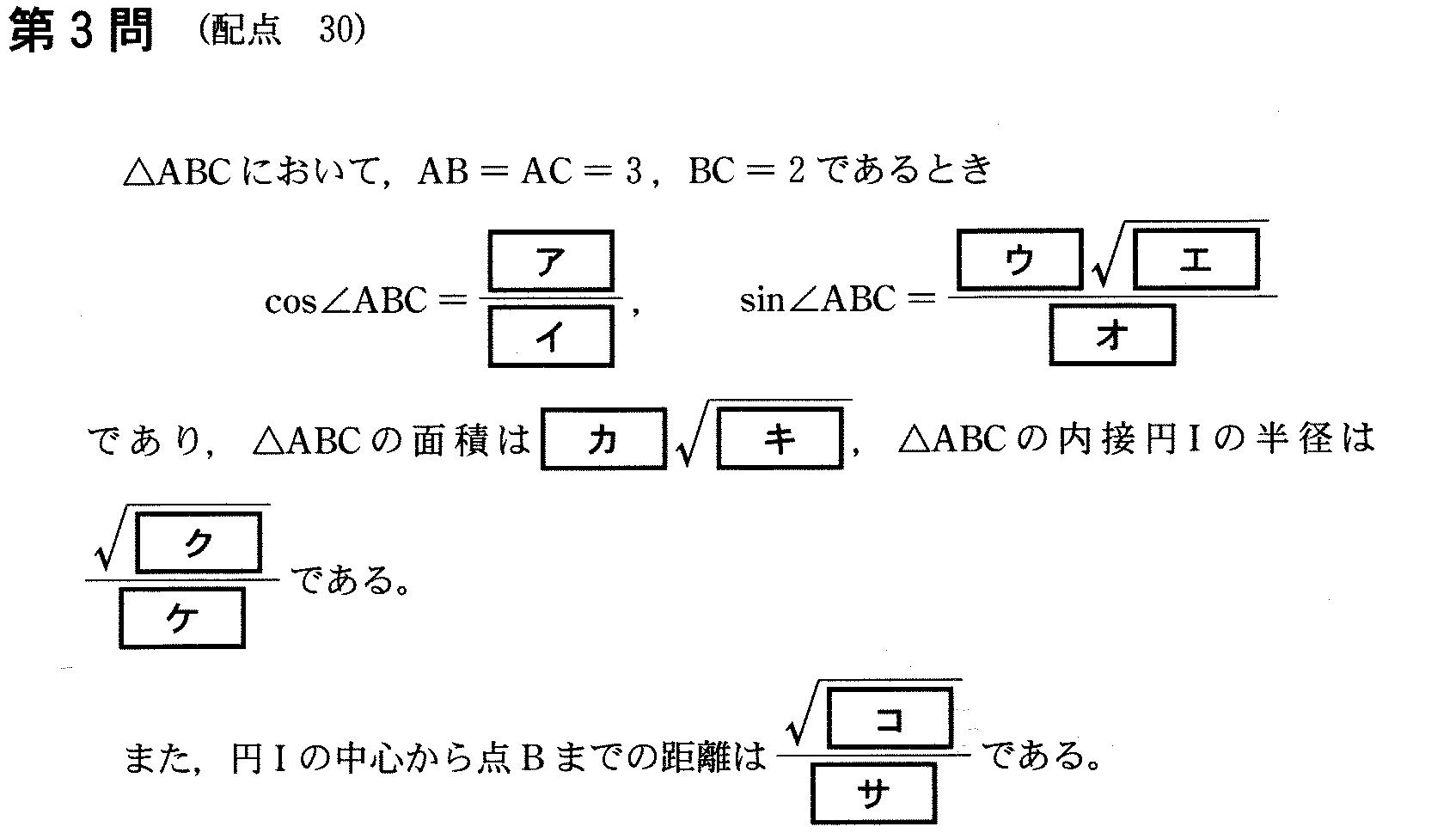 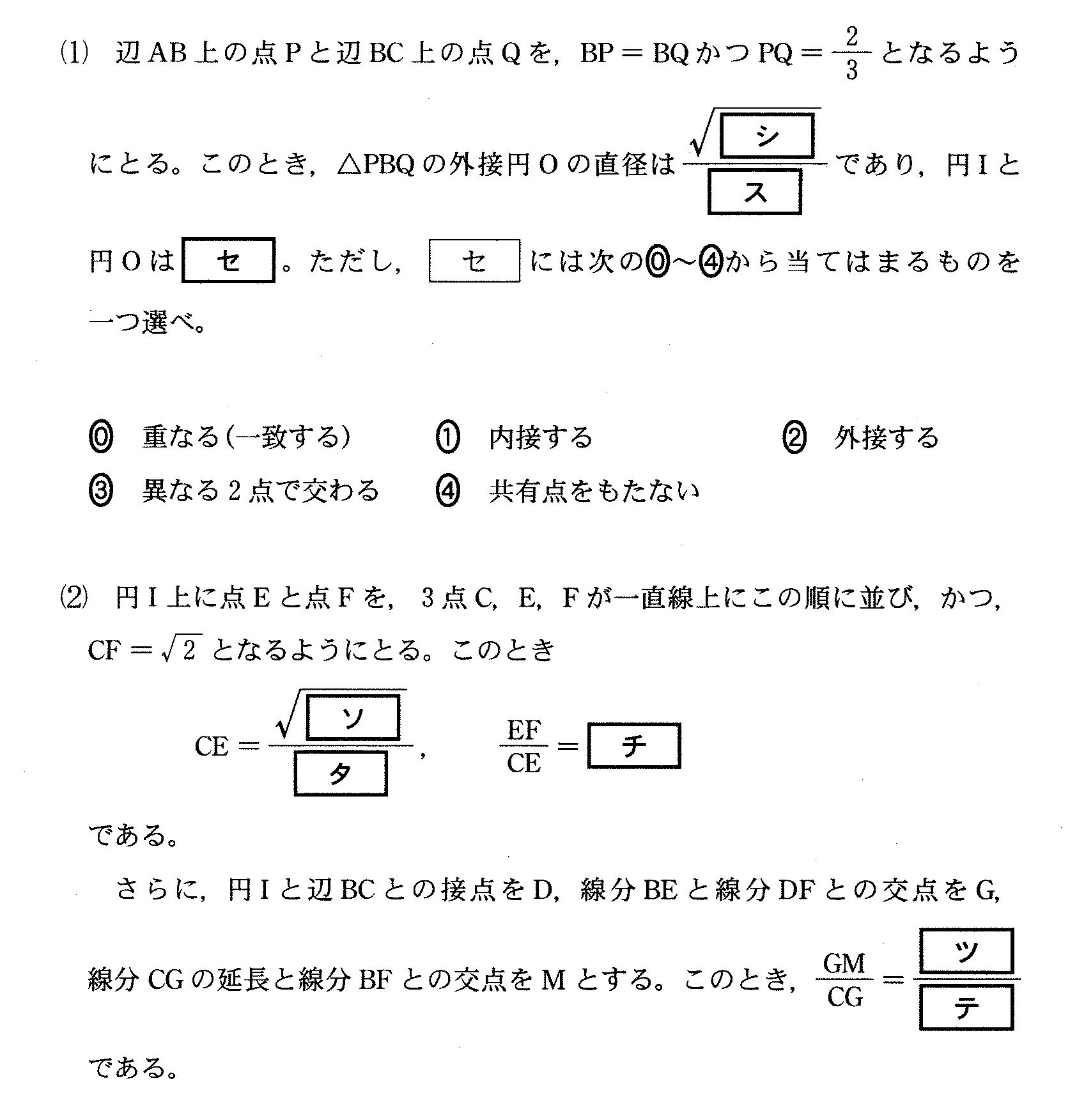  第3問 cos∠ABC求めるんだけど、△ABCの全部の辺の長さわかってるんだから、余弦定理を使うってわかる。 余弦定理使ってcos∠ABC=1/3を得る。 sinの方はsin^2+cos^2=1より sin∠ABC=±2√2/3 0≦∠ABC≦180°ゆえsinは正だからプラスの方が答え。 △ABCの面積は公式つかって=1/2*AB*BC*sinB=2√2 BCの中点Dとする △ABDに着目してAD=√8=2√2 また内接円の半径をx、 中心をOとすると、AO=2√2 ーx △AONで三平方の定理より (2√2ーx)^2=4+x^2 とくとx=√2/2 OBの距離は△OBDで三平方よりOB=√(1+1/2)=√6/2 (1)外接円ときたら、 公式sin<ABC/AC=1/2Rを思い出す。 これを△PQBに適用して sinB/PQ=1/2R R=√2/4 円OはB通らない。円IはB通るから、一致はありえない。 また図描いてみたらだいたい異なる2点で交わるくらいだとわかる。Bからの距離とか調べて正確なこと求めた方がいいんだろうけど、時間制限もあるのでこのへんは直観でいいとおもう。 (2) 図をかいてみると △CFOで余弦定理つかってcos∠ECOもとめて △CEOで再び余弦定理によりCE求めてやると思いつく。こういう問題は、 ∠ECO=αとおいて △CFOで余弦より 1/2=3/2+2ー2√2√3/√2*cosα とくと cosα=√3/2 次に△CEOで、CE=yとおいて余弦より 1/2=3/2+y^2ー2y√3/√2*cosα yの2次方程式とくと y=√2、1/√2 CE<√2ゆえ CE=√2/2 EF/CE=1もすぐわかる。 E,Dは中点であるから、Gは重心である。だからCG:GM=2:1 ホームへ戻る |