
|
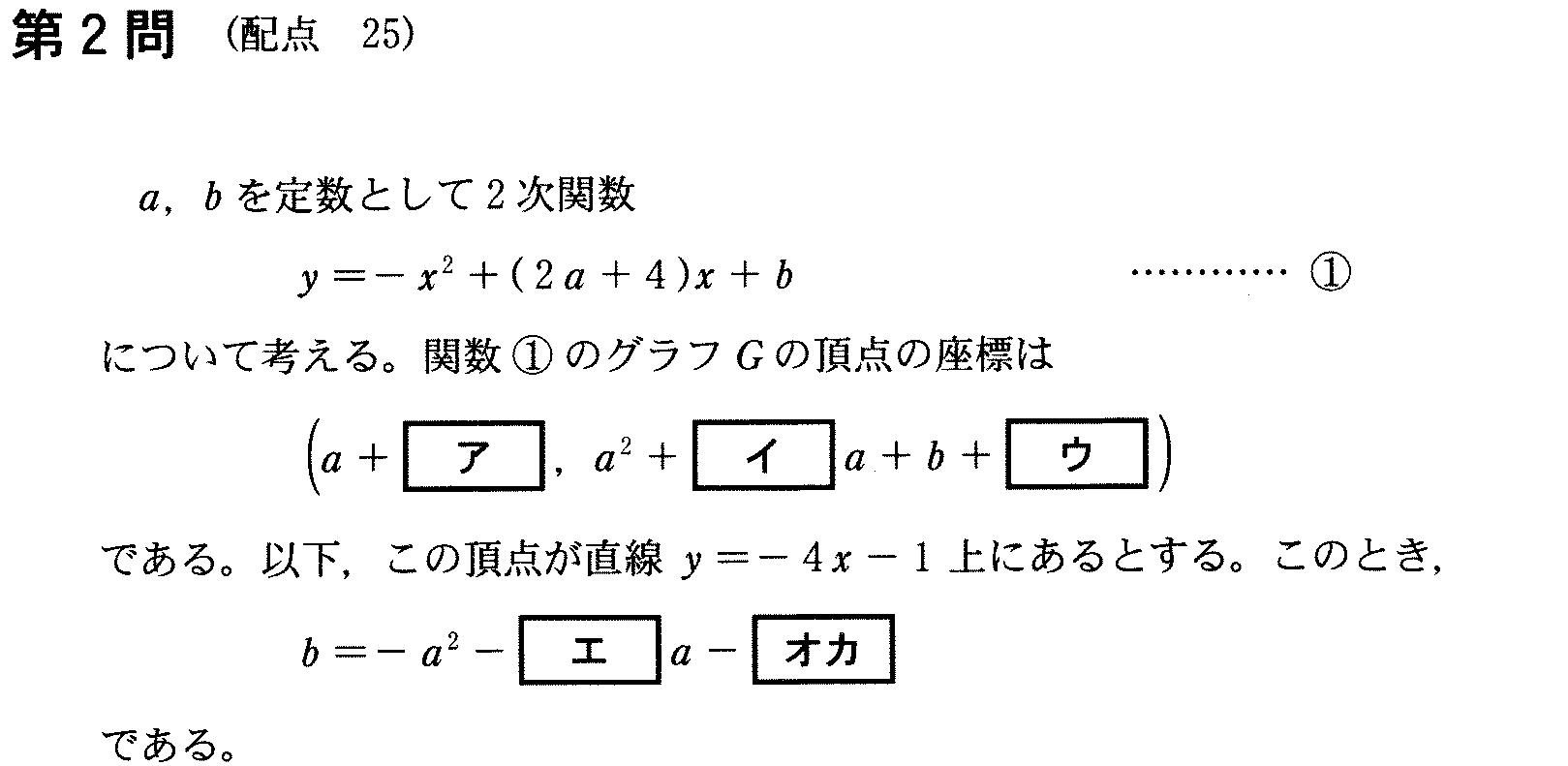 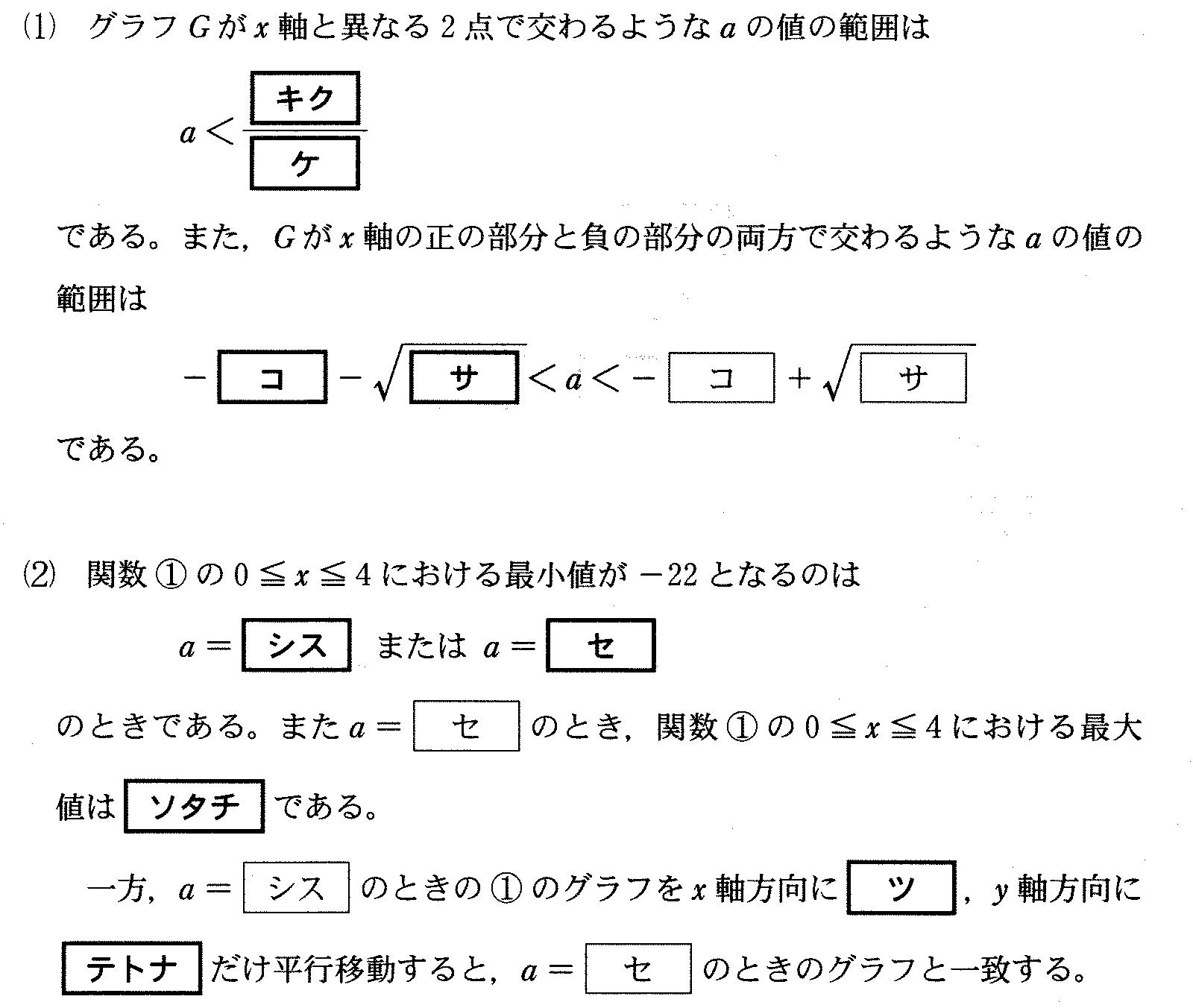  戞俀栤 偙傟傕枅擭偺傛偆偵偱傞栤戣丅 嘆傪曄宍偟偰捀揰傕偲傔傞丅 億僀儞僩偼 丒俀師偺學悢偑晧偺帪偼侾師偺崁偲堦弿偵偐偭偙偱偔偔偭偰 丒偐偭偙撪傪暯曽姰惉丅 偙傟偼偄偮傕摨偠僷僞乕儞側偺偱妎偊偰偍偔丅 嬶懱揑偵偐偔偲丄 倷亖乕乷倶丱俀乕乮俀倎亄係乯倶乸亄倐 丂亖乕乷乮倶乕乮倎亄俀乯乯丱俀乕乮倎亄俀乯丱俀乸亄倐 丂亖乕乮倶乕乮倎亄俀乯乯丱俀亄乮倎亄俀乯丱俀亄倐 偙偆偟偰捀揰偼乮倎亄俀丄倎丱俀亄係倎亄係亄倐乯偲側傞丅 傑偨偙偺捀揰偑倷亖乕係倶乕侾忋偵偁傞備偊 捀揰偺嵗昗傪戙擖偡傟偽傛偄丅 傛偭偰倐亖乕倎丱俀乕俉倎乕侾俁 乮侾乯 倶幉偲堎側傞俀揰偱岎傢傞丅 偙傟傕寛傑偭偨傗傝曽丅敾暿幃亜侽丅 敾暿幃俢亖乮俀倎亄係乯丱俀乕係乮乕侾乯倐亜侽 慜偺倐傪戙擖偟偰夝偔偲 倎亙乕俋乛係 師偵丄俧偑倶幉偺惓偺晹暘偲晧偺晹暘椉曽偱岎傢傞偐傜丄 僌儔僼傪僀儊乕僕偟側偑傜丄僌儔僼偼忋偵撌偱偁傝丄 偮傑傝倖乮侽乯亜侽偲偄偆偙偲偩偲傢偐傞丅乮倷亖倖乮倶乯偲偟偰偍偔乯偙傟傕寛傑偭偨傗傝曽側偺偱妎偊偲偔丅 偙傟傪夝偔偲僐偲僒偼摼傜傟傞丅 乮俀乯 侽亝倶亝係偵偍偗傞嵟彫抣偑乕俀俀丅 僌儔僼偑忋偵撌偩偐傜嵟彫抣偲傞偺偼倖乮侽乯偐倖乮係乯偩偲傢偐傞丅 偟偐偟偳偭偪偐傢偐傜側偄丅 偙偆偲偒偼応崌暘偗丅 倖乮侽乯偑倖乮係乯傛傝壓偵側傞応崌偲 倖乮係乯偑倖乮侽乯傛傝壓偵側傞応崌 偙傟偼偮傑傝侽偲係偺拞娫揰俀偑偙偺僌儔僼偺幉傛傝嵍偵偁傞偐塃偵偁傞偐偱暘偗傞丅 乮倎乯俀亙倎亄俀偺偲偒丂乮侽亙倎乯 倖乮侽乯偱嵟彫抣乕俀俀偲傞丅 夝偔偲 倎亖侾丄乕俋丂侽亙倎枮偨偡偺偼倎亖侾 乮倐乯俀亜倎亄俀偺偲偒丂乮侽亜倎乯 倖乮係乯偱嵟彫抣乕俀俀偲傞丅 夝偔偲 倎亖亇俁丂丂侽亜倎枮偨偡偺偼倎亖乕俁 倎亖侾偺偲偒捀揰乮俁丄乕侾俁乯偱偁傝丄侽亝倶亝係偺嵟戝抣偼乕侾俁 倎亖乕俁偺偲偒捀揰偼乮乕侾丄俁乯 偙偆偄偆暯峴堏摦偺栤戣偱偼捀揰偺傒偵拝栚偡傟偽傛偄丅 偮傑傝捀揰偺堏摦偼倶曽岦偵係丄倷曽岦偵乕侾俇 儂乕儉傊栠傞 |